eda
This keyword specifies the method used to perform an Energy Decomposition Analysis (EDA) calculation.
Options
type
Both GKS-EDA and TSO-EDA are available for analyzing intermolecular interactions.
Furthermore, when combined with the many-body expansion scheme, two extended methods—many-body GKS-EDA and many-body TSO-EDA—are available for analyzing many-body interactions.
In Qbics, it is recommended to use TSO-EDA for Energy Decomposition Analysis (EDA) calculations.
| Value | tso for block localized wavefunction energy decomposition analysis (TSO-EDA). |
gks for generalized Kohn-Sham energy decomposition analysis (GKS-EDA). |
|
mb_tso for many-body interaction TSO-EDA. |
|
mb_gks for many-body interaction GKS-EDA. |
|
| Default | None |
frag
This option defines the fragment partitioning of a system. The format is:
frag num_electrons spin_multiplicity atom_range
This format is the same as used for the frag keyword in the scfguess option. See the scfguess documentation for more details.
nobsse
Disable the Boys and Bernardi counterpoise (CP) correction for basis set superposition error (BSSE). By default, Qbics performs BSSE correction automatically. Use this keyword to disable the correction if BSSE is not to be considered in your calculation.
tso_for_guess
Perform a TSO calculation first to generate the initial guess for the fragments' wavefunctions.
This step is necessary when fragments have C∞ symmetry, such as isolated atoms.
For tso and mb_tso, this is the default behavior.
mb_level
| Value | An integer |
| Default | 2 |
Specifies the truncation level for many-body interaction analysis, used in mb_gks and mb_tso calculations.
The value must be no less than 2 and should be equal to or greater than the number of fragments.
Typically, a value of 4 is recommended if the number of fragments exceeds 4.
Higher-order interaction terms beyond this are usually negligible and can be safely ignored.
For EDA tasks, be sure to include type U in the scf keyword to enable unrestricted calculations.
Otherwise, the calculation will fail.
Theoretical Background
If you use tso or mb_tso, please cite the following references:
If you use gks or mb_gks, please cite the following reference:
TSO-EDA
TSO-EDA is based on the Target State Optimization self-consistent field method (J. Chem. Theory Comput. 2023, 19, 1777) and decomposes the total interaction energy into five terms: electrostatic, exchange, polarization, charge transfer, and dispersion energies. The sum of electrostatic and exchange energy is referred to as the Heitler–London term (Phys. Chem. Chem. Phys. 2024, 26, 17549).
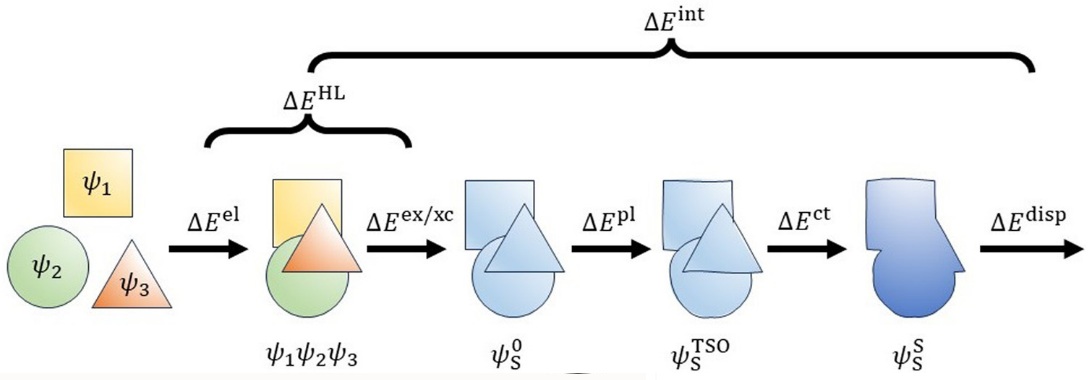
The energy terms in TSO-EDA are defined as follows:
- Electrostatic term: Represents the semiclassical Coulombic interaction between charged particles from different monomers.
- Exchange term: Accounts for quantum effects arising from the antisymmetric nature of the electronic wavefunction and the Pauli exclusion principle.
- Polarization term: Describes the polarization of the electron density of one monomer due to the presence of another.
- Charge transfer term: Represents the transfer of electronic charge between monomers.
- Dispersion term: Represents dispersion (van der Waals) interactions between monomers.
The basis set superposition error (BSSE) is included in the charge transfer term. All of the above energy components can be found in the Qbics output.
Many-Body TSO-EDA
This method, developed in Phys. Chem. Chem. Phys. 2024, 26, 17549, is used to analyze many-body effects in molecular clusters. The total interaction energy is decomposed into two-body, three-body, and higher-order contributions, as follows:
$$\Delta E^{\text{int}} = \frac{1}{2!} \sum_{I_1 \neq I_2}^{N} \Delta E_{I_1 I_2}^{(2)} +\frac{1}{3!} \sum_{I_1 \neq I_2 \neq I_3}^{N} \Delta E_{I_1 I_2 I_3}^{(3)} + \cdots + \frac{1}{n!} \sum_{I_1 \neq \cdots \neq I_n}^{N} \Delta E_{I_1 \cdots I_n}^{(n)} + \cdots + \Delta E_{I_1 \cdots I_N}^{(N)} \equiv \sum_{n=2}^{N} \Delta E^{(n)}$$
Terms beyond \( \Delta E^{(2)} \) represent many-body interaction effects. Among these, the three-body term \( \Delta E^{(3)} \) is usually the most significant. Its behavior can be categorized into three types:
- \( \Delta E^{(3)} < 0 \): Indicates a cooperative effect among monomers. The many-body interaction stabilizes the cluster. This is commonly observed in hydrogen-bonded systems, such as water clusters.
- \( \Delta E^{(3)} > 0 \): Indicates an anti-cooperative effect. The many-body interaction destabilizes the cluster. This often occurs in clusters of charged species, such as ionic liquid clusters. (See discussion below.)
- \( \Delta E^{(3)} \approx 0 \): Indicates a non-cooperative effect. There is minimal many-body interaction in the system. This is typical for clusters without significant charge or hydrogen bonding.
Each order can be decomposed into electrostatic, exchange, polarization, charge transfer, and dispersion components.
$$\Delta E_X^{(n)} = \Delta E_X^{(n)\text{-el}} + \Delta E_X^{(n)\text{-ex/xc}} + \Delta E_X^{(n)\text{-pl}} + \Delta E_X^{(n)\text{-ct}} + \Delta E_X^{(n)\text{-disp}}$$
Electrostatic and exchange terms are typically highly additive, whereas polarization and charge transfer terms are non-additive. The dispersion term is consistently additive.
Input Examples
Example: EDA for GeH3F-NCH Complex by B3LYP-D3BJ/def2-SVP
For the GeH3F–NCH complex, an EDA calculation can be performed using the following input:
mol
Ge 0.00000000 0.00221863 -0.79935317
H 0.00000000 1.48645043 -0.40384625
H 1.28514604 -0.74161126 -0.40477816
H -1.28514603 -0.74161126 -0.40477816
F 0.00000000 0.00108752 -2.56116087
C 0.00000000 -0.00225138 3.35662076
H 0.00000000 -0.00220444 4.43604901
N 0.00000000 -0.00207825 2.20326200
end
basis
def2-svp
end
scf
charge 0
spin2p1 1
type U # For EDA calculations, this must be added explicitly.
end
grimmedisp
type bj
end
eda
type tso # You can also change it to: gks
frag 0 1 1-5 # Define GeH3F.
frag 0 1 6-8 # Define HCN.
end
task
eda b3lyp
endThe atom indices are shown below:
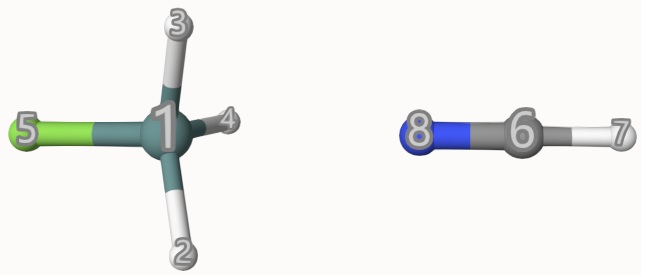
The results are:
WITH BSSE correction:
Electrostatic interaction energy: -4.98 kcal/mol
Exchange-correlation interaction energy: 4.22 kcal/mol
Polarization interaction energy: -0.62 kcal/mol
Charge transfer interaction energy: -1.31 kcal/mol
Grimme's dispersion interaction: -1.58 kcal/mol
----------------------------------------------------------------
Total interaction energy: -4.27 kcal/molThe total interaction energies—both with and without BSSE correction—are identical for the TSO-EDA and GKS-EDA methods, although their individual energy components differ. As noted earlier, Qbics recommends using TSO-EDA. In this complex, stabilization is dominated by the electrostatic term, which accords with the chemical intuition that σ-hole interactions are responsible for its binding.
Example: MB-EDA for Molecular Cluster (NH4+)2(H2SO4)(HSO4-)2
The cluster of interest contains two NH4+ cations, one H2SO4 molecule, and two HSO4− anions. This ion–molecule assembly is frequently investigated in atmospheric-chemistry studies. An MB-EDA analysis can be launched with the following input:
basis
def2-svp
end
scf
charge 0 # Total charge.
spin2p1 1
type U
end
grimmedisp
type bj
end
eda
type mb_tso
mb_level 4
frag +1 1 1-5 # NH4+
frag +1 1 6-10 # NH4+
frag 0 1 11-17 # H2SO4
frag -1 1 18-23 # HSO4-
frag -1 1 24-29 # HSO4-
end
mol
N 0.13124700 -1.86033100 -1.49054300
H -0.68471400 -1.96085700 -0.84840100
H 0.16284500 -2.63375000 -2.14527600
H -0.00155300 -0.97157900 -1.98611500
H 1.02982000 -1.79400200 -0.97437700
N -1.89606400 2.02266900 1.95536400
H -2.33766600 1.07911300 1.78190600
H -1.20423600 1.92734800 2.69193100
H -1.40455300 2.34660500 1.08417600
H -2.60508400 2.69280200 2.23215700
S 3.40269500 -0.73966700 0.43845300
O 4.56636300 -1.26003200 1.03924300
O 2.66268100 -1.55477200 -0.49575900
O 2.42657400 -0.30120000 1.56959800
O 3.78755300 0.58843400 -0.27018200
H 2.99297400 1.01172300 -0.68798600
H 1.56137200 -0.00498400 1.17228000
S -3.05756300 -0.82805000 0.17173500
O -2.21824200 -1.98280100 -0.09354400
O -3.00471800 -0.39464500 1.56194000
O -2.90973700 0.26502300 -0.77053900
O -4.55472700 -1.30387800 -0.08712900
H -4.73898300 -2.05912100 0.48328300
H -1.51856700 0.72871100 -1.53329100
S 0.24159900 1.52238500 -0.65825900
O -0.59336700 0.90131200 -1.85962900
O 1.55183900 1.72430300 -1.22252400
O -0.45708500 2.72297400 -0.23978600
O 0.20716100 0.49864900 0.39894800
end
task
eda b3lyp
end The atom indices listed below are used to define the frag fragments.
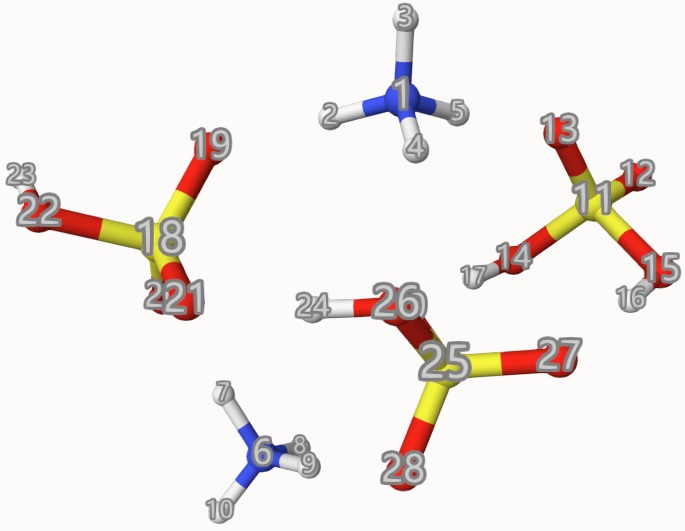
The results are as follows:
Table 5. Summary (kcal/mol).
---------------------------------------------------------------------------------------------------------------------------------
Interactions delE_el delE_xc delE_pl delE_ct delE_bsse delE_disp delE_tot
---------------------------------------------------------------------------------------------------------------------------------
SUM of 2-body -3.51853640E+02 1.04231044E+02 -5.50310217E+01 -9.70290703E+01 4.35696096E+01 -1.98079059E+01 -3.75920984E+02
SUM of 3-body 1.72107484E-09 1.45358519E+00 2.82254671E+01 2.81735373E+01 -1.24450163E+01 1.01531078E-02 4.54177264E+01
SUM of 4-body -4.14670076E-09 1.70212282E-02 -2.25462767E+00 -5.15894065E+00 1.89758583E+00 2.28017787E-05 -5.49893846E+00
Remain 7.51748885E-09 -8.58522126E-04 6.43113307E-02 4.30266615E-01 -1.22896862E-01 5.97720460E-07 3.70823167E-01
---------------------------------------------------------------------------------------------------------------------------------
SUM -3.51853640E+02 1.05700792E+02 -2.89958710E+01 -7.35842070E+01 3.28992822E+01 -1.97977294E+01 -3.35631373E+02
---------------------------------------------------------------------------------------------------------------------------------The total interaction energy is −335.63 kcal mol−1, resolved into two-, three-, four-, and higher-order contributions:
- Two-body: −375.92 kcal mol−1 — the dominant, stabilising term.
- Three-body: +45.42 kcal mol−1 — substantial yet anti-cooperative, thus destabilising the complex.
- Four-body: −5.50 kcal mol−1 — small and slightly cooperative.
- Five- plus six-body (remainder): +0.37 kcal mol−1 — negligible.
Electrostatic and exchange contributions are strongly additive, whereas polarization and charge-transfer contributions are distinctly non-additive. The magnitude and sign of three-body (many-body) effects vary markedly across different cluster types; see Phys. Chem. Chem. Phys. 2024, 26, 17549 for details.