basinfo
This keyword specifies the implementation details of the basis functions.
Options
angular_type
| Value | Cartesian. Uses Cartesian basis sets (e.g., 6d/10f/15g) . |
spherical. Uses spherical harmonic basis sets (e.g., 5d/7f/9g). |
|
| Default | spherical |
Use spherical or Cartesian GTO basis sets.
Spherical is recommended; Cartesian is typically for testing only.
linear_dependence
| Value | A real number |
| Default | 1.E-8 |
Assign the threshold for detecting linear dependence in the basis set. Must be a positive real number. Qbics will stop and raise an error if linear dependence is found.
Linear dependence may occur when:
- Identical basis functions are assigned to the same nucleus.
- Two identical atoms are placed too close together.
- Too many diffuse functions are used in a large molecule.
ghost
| Value | Atom range |
| Default | None |
Assigning "ghost atoms" means the atoms have basis functions but no nuclei or electrons. Commonly used in BSSE calculations, though Qbics handles this automatically.
Theoretical Background
Angular Type of Basis Functions
The analytical form of a Gaussian basis function is:
$$\chi(\mathbf{r}) = A_{L}(\mathbf{r})\sum_{k=1}^{K} C_k e^{-\alpha_k r_{A}^2}$$
-
Here,
- \( A_L(\mathbf{r}) \) is the angular part with angular momentum quantum number \( L \).
- \( K \) is the contraction degree.
- \( \alpha_k \) is the exponent.
- \( C_k \) is the contraction coefficient.
- \( \mathbf{A} \) is the position of the atom.
-
The angular part \( A_L(\mathbf{r}) \) has two forms:
Cartesian: expressed as \( x_A^l y_A^m z_A^n \).spherical: given by a real solid spherical harmonic function.
Spherical basis sets are more compact and efficient for quantum chemical calculations.
Ghost Atoms
In quantum chemistry, ghost atoms are atoms that have basis functions but no nuclei or electrons. They are commonly used in basis set superposition error (BSSE) calculations to evaluate the interaction between two molecules. Ghost atoms help eliminate the artificial interaction caused by overlapping basis functions.
Although BSSE can be calculated manually using the ghost option, this is usually unnecessary. Qbics handles it automatically through energy decomposition analysis (EDA).
Input Examples
Example: GeH3F-NCH with Ghost Atoms
For the complex GeH3F-NCH, calculate the energy with HCN treated as a ghost molecule at the B3LYP/def2-SVP level of theory.
basis
def2-svp
end
basinfo
ghost 6-8 # The indices of HCN.
end
scf
charge 0
spin2p1 1
type R
end
mol
Ge 0.00000000 0.00221863 -0.79935317
H 0.00000000 1.48645043 -0.40384625
H 1.28514604 -0.74161126 -0.40477816
H -1.28514603 -0.74161126 -0.40477816
F 0.00000000 0.00108752 -2.56116087
C 0.00000000 -0.00225138 3.35662076
H 0.00000000 -0.00220444 4.43604901
N 0.00000000 -0.00207825 2.20326200
end
task
energy b3lyp
endThe ghost keyword indicates that atoms 6, 7, and 8 (i.e., C, H, and N) are treated as ghost atoms.
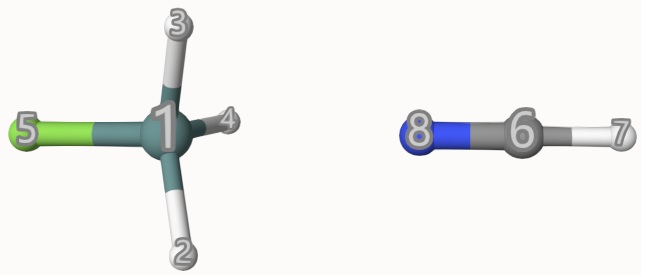
In the output, you can see:
# of ghost atoms: 3
Indices: 6 7 8
Sum of ghost atom electrons: 14
...
SCF Structure:
# of electrons: 44
# of alpha electrons: 22
# of beta electrons: 22
2S+1: 1The ghost atoms are listed, and the total number of electrons is 44 — exactly matching the electron count of GeH3F, confirming that HCN is treated as a ghost molecule.