Tip
All input files can be downloaded: Files.
Tip
For detailed tutorials of MSDFT, please refer to the following ones:
msdft
This option defines the implementation details of multi-state density functional theory (MSDFT) for excited and diabaitc states.
- offdiag_correlation
Value
overlap_weightedWill use overlap weighted methodenergy_weightedWill use energy weighted methodcorrelation_potentialWill use correlation functional method, given by thexc_functionaloptionDefault
overlap_weightedDefine the off-diagonal correlation method.
- single_ex
Value
Single excitations to be considered
Default
None
This option indicates what single excitations are considered.
The input format is:
single_ex occupied_MO_incides : virtual_MO_indicesFor example,
single_ex 1 5-6 9 : 10-13 15considers the following single excitations:1 → 10
1 → 11
1 → 13
1 → 15
5 → 10
5 → 11
5 → 13
5 → 15
6 → 10
6 → 11
6 → 13
6 → 15
9 → 10
9 → 11
9 → 13
9 → 15
- double_ex
Value
Double excitations to be considered
Default
None
This option indicates what double excitations are considered.
The input format is:
double_ex occupied_MO_incides : virtual_MO_indicesFor example,
double_ex 1 5-6 9 : 10-13 15considers the following double excitations:1 → 10
1 → 11
1 → 13
1 → 15
5 → 10
5 → 11
5 → 13
5 → 15
6 → 10
6 → 11
6 → 13
6 → 15
9 → 10
9 → 11
9 → 13
9 → 15
Theoretical Background
XXXXXX
Input Examples
Tip
For detailed tutorials of MSDFT, please refer to the following ones:
Example: Excited States of (E)-Dimethyldiazene (Automatically)
In this example, we will calculate the ground state and 2 singlet excited states of (E)-Dimethyldiazene with MSDFT methods. We will use B3LYP/cc-pVTZ level of theory.
Tip
Acutally, in Qbics, the calculation of excited states using MSDFT is close to (but NOT the same as) TSO+NOSI. See scfguess and nosi for details.
The input file is:
1basis
2 cc-pvtz
3end
4
5scf
6 charge 0
7 spin2p1 1
8 type U
9end
10
11mol
12 N -0.11855722 0.06367877 -0.00010027
13 N 1.11855814 -0.06366086 -0.00010026
14 C 1.81864333 1.22402113 0.00009549
15 H 1.12816980 2.07452976 0.00011126
16 H 2.46787129 1.25512096 0.88302715
17 H 2.46820089 1.25538193 -0.88260363
18 C -0.81864582 -1.22402070 0.00009559
19 H -0.12816015 -2.07453667 0.00011125
20 H -1.46787530 -1.25512668 0.88303320
21 H -1.46820496 -1.25538766 -0.88260977
22end
23
24msdft
25 single_ex 15 16 : 17
26end
27
28task
29 msdft b3lyp
30end
Here, single_ex 15 16 : 17 indicates that 1 electron in the 15th or 16th MO is excited to the 17th MO, i.e.:
15 → 17
16 → 17
In msdft...end, there is no offdiag_correlation option. This means that the off-diagonal correlation will be calculated using the (default) overlap weighted method.
After calculation, we will obtain the output file msdft-1.out and wavefunction files msdft-1-gs.mwfn, msdft-1-15-to-17-se.mwfn, msdft-1-16-to-17-se.mwfn. etc. Their names are self-explaining. For example, msdft-1-15-to-17-se.mwfn is the wavefunction file for the single excitation from 15th to 17th MO.
In the output file msdft-1.out, we can find the following information:
1Read non-orthogonal determinants:
20 msdft-1-gs.mwfn
31 msdft-1-15-to-17-se.mwfn
4Spin flipped: msdft-1-15-to-17-se.mwfn
52 msdft-1-16-to-17-se.mwfn
6Spin flipped: msdft-1-16-to-17-se.mwfn
7
8---- NOSI Overlap Matrix ----
9=============================
10 0 1 2 3 4
11 0 1.00000000 0.00000000 0.00004807 0.00000000 0.00000778
12 1 0.00000000 1.00000000 0.00000000 0.00000000 0.00000000
13 2 0.00004807 0.00000000 1.00000000 0.00000000 0.00000000
14 3 0.00000000 0.00000000 0.00000000 1.00000000 0.00000000
15 4 0.00000778 0.00000000 0.00000000 0.00000000 1.00000000
16
17---- NO Hamiltonian Matrix Functional ----
18==========================================
19 0 1 2 3 4
20 0 -189.34737100 0.00000019 -0.00909719 -0.00000028 -0.00147274
21 1 0.00000019 -189.11479500 0.09271220 -0.00000307 -0.00000741
22 2 -0.00909719 0.09271220 -189.11479500 -0.00000741 -0.00000307
23 3 -0.00000028 -0.00000307 -0.00000741 -189.24112500 0.02098466
24 4 -0.00147274 -0.00000741 -0.00000307 0.02098466 -189.24112500
25
26---- NOSI Coefficients Matrix (column vectors are eigenvectors) ----
27====================================================================
28 0 1 2 3 4
29 0 -1.00000000 -0.00000085 -0.00000551 -0.00001218 -0.00002378
30 1 -0.00000820 0.00005595 0.00003731 -0.70710678 0.70710678
31 2 0.00002264 -0.00005595 0.00003731 0.70710678 0.70710678
32 3 -0.00000330 -0.70710678 0.70710678 -0.00005595 -0.00003731
33 4 0.00000328 0.70710678 0.70710678 0.00005595 -0.00003731
34
35---- Singlet and Triplet Excitation Energies ----
36=================================================
37Eigenstate 0: -189.34737100 Hartree; Excitation energy: 0.00000000 eV
38Eigenstate 1: -189.26210966 Hartree; Excitation energy: 2.32008047 eV
39Eigenstate 2: -189.22014034 Hartree; Excitation energy: 3.46212432 eV
40Eigenstate 3: -189.20750727 Hartree; Excitation energy: 3.80588786 eV
41Eigenstate 4: -189.02208273 Hartree; Excitation energy: 8.85154931 eV
42
43---- Singlet State Weights ----
44===============================
45 0 1 2 3 4
46 0 1.00000000 -0.00000000 0.00000000 -0.00000000 -0.00000000
47 1 0.00000000 0.00000000 0.00000000 0.50000000 0.50000000
48 2 -0.00000000 0.00000000 0.00000000 0.50000000 0.50000000
49 3 0.00000000 0.50000000 0.50000000 0.00000000 0.00000000
50 4 -0.00000000 0.50000000 0.50000000 0.00000000 0.00000000
51
52---- NOSI Results ----
53======================
54 State NOSI Energies Excited Energy Osc. Str. DX DY DZ
55 (Hartree) (eV) (a.u.) (a.u.) (a.u.)
56 0 -189.34737100 0.00000000 0.00000000 42.82334 0.00028 0.00212
57 1 -189.26210966 2.31996110 0.00000000 0.00000 -0.00000 -0.00001
58 2 -189.22014034 3.46194620 0.00000000 -0.00000 0.00005 0.00001
59 3 -189.20750727 3.80569205 0.00000000 -0.00000 -0.00000 -0.00000
60 4 -189.02208273 8.85109391 0.94030373 2.85146 0.75306 0.00000
In Read non-orthogonal determinants:, the determinants are shown:
\(\phi_0\) msdft-1-gs.mwfn
\(\phi_1\) msdft-1-15-to-17-se.mwfn
\(\phi_2\) msdft-1-15-to-17-se.mwfn (spin flipped)
\(\phi_3\) msdft-1-16-to-17-se.mwfn
\(\phi_4\) msdft-1-16-to-17-se.mwfn (spin flipped)
In NOSI Overlap Matrix, the matrix elements \(\left\langle\phi_i\middle|\phi_j\right\rangle\) are calculated.
In NO Hamiltonian Matrix Functional, the matrix elements \(\left\langle\phi_i\left|\hat{H}\right|\phi_j\right\rangle\) are calculated.
In NOSI Coefficients Matrix, the column vectors are eigenvectors of the NOSI Hamiltonian matrix. For example, in column 1, we have:
When a determinant and its spin flipped counterpart are combined with out-of-phases (-0.70710678 and -0.70710678), this is a triplet state. When a determinant and its spin flipped counterpart are combined with in-phases (0.70710678 and 0.70710678), this is a singlet state.
The excited energies are shown in NOSI Results.
A CI coefficient file and a spectrum file are generated. For example, msdft-1-ci.txt and msdft-1-spectrum.txt.
You can see that the energies are slightly different from the results obtained by TSO+NOSI in nosi. This is because the MSDFT method applied triplet correction, which should be more accurate.
State |
MSDFT (eV) |
TSO+NOSI (eV) (see nosi) |
S0 |
0.00000000 |
0.00000000 |
T1 |
2.31996110 |
2.32371833 |
S1 |
3.46194620 |
3.45818894 |
T2 |
3.80569205 |
3.82320418 |
S2 |
8.85109391 |
8.83363623 |
Example: N and O K-Edge XAS of N2O
In this example, we will calculate the K-edge XAS of N2O with MSDFT methods. We will use B3LYP/cc-pCVTZ level of theory. Here, “K-edge” means that the excitation is from 1s orbital to virtual ones. We use aug-cc-pCVTZ instead of aug-cc-pVTZ because the “pCVTZ” is highly optimized for core orbitals.
First, we do a standard SCF calculation for N:sub:`2`O to see orbitals. The input file is:
1basis
2 aug-cc-pCVTZ
3end
4
5scf
6 charge 0
7 spin2p1 1
8 type U
9end
10
11mol
12 N 0. 0. -0.14168067
13 N 0. 0. 0.97956073
14 O 0. 0. 2.16211994
15end
16
17task
18 energy b3lyp
19end
Now we can visualize the molecular orbitals. Open Qbics-MolStar, and drag n2o-gs.mwfn into explorer, and it will be automatically loaded. Right-click n2o-gs.mwfn and select View Molecular Orbitals. Click the MOs and see below:
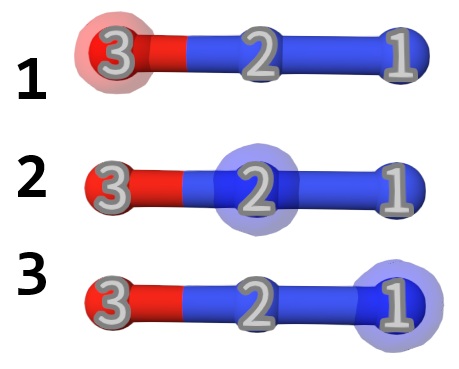
Obviously, the MO 1 is the 1s orbitals for oxygen, and the MO 2,3 are the 1s orbitals for nitrogen. The N and O K-edge XAS are quiet separated, so it is better (but not necessary) to calculate them separately with MSDFT methods. The input files for O and N K-edge XAS are:
1basis
2 aug-cc-pCVTZ
3end
4
5scf
6 charge 0
7 spin2p1 1
8 type U
9end
10
11mol
12 N 0. 0. -0.14168067
13 N 0. 0. 0.97956073
14 O 0. 0. 2.16211994
15end
16
17msdft
18 single_ex 1 : 12-18
19end
20
21task
22 msdft b3lyp
23end
1basis
2 aug-cc-pCVTZ
3end
4
5scf
6 charge 0
7 spin2p1 1
8 type U
9end
10
11mol
12 N 0. 0. -0.14168067
13 N 0. 0. 0.97956073
14 O 0. 0. 2.16211994
15end
16
17msdft
18 single_ex 2 3 : 12-18
19end
20
21task
22 msdft b3lyp
23end
Here, single_ex 1 : 12-18 indicates that 1 electron in the 1st MO is excited to the 12th to 18th MO; single_ex 2 3 : 12-18 indicates that 1 electron in the 2nd and 3rd MO is excited to the 12th to 18th MO. You can excite them to higher virtual MOs to get more accurate results.
After calculation, we will obtain the output files msdft-2-O.out and msdft-2-N.out. The excited state MWFN files are also available. There are also files for spertrum plotting: msdft-2-O-spectrum.txt and msdft-2-N-spectrum.txt.
For example, in msdft-2-N.out, we can find the following information:
1---- NOSI Results ----
2======================
3 State NOSI Energies Excited Energy Osc. Str. DX DY DZ
4 (Hartree) (eV) (a.u.) (a.u.) (a.u.)
5 0 -184.74191466 0.00000000 0.00000000 -0.00000 0.00001 62.02962
6 1 -170.03989460 400.04196592 0.00000000 0.00000 -0.00000 0.00000
7 2 -170.03502387 400.17449843 0.00000000 -0.00000 0.00000 -0.00000
8 3 -170.01752034 400.65076950 0.05261600 0.06433 0.08133 0.00000
9 4 -170.01547342 400.70646604 0.05144446 0.08040 -0.06362 -0.00000
10 5 -169.92447560 403.18251673 0.00000000 0.00000 -0.00000 0.00000
11 6 -169.91893969 403.33314900 0.00000000 0.00000 -0.00000 -0.00000
12 7 -169.91191435 403.52430858 0.00000000 -0.00000 0.00000 0.00000
13 8 -169.91076621 403.55554928 0.00534389 0.00000 -0.00000 0.03293
14 9 -169.88759854 404.18594177 0.06488836 -0.07104 -0.08999 0.00000
15 10 -169.88267696 404.31985772 0.06490275 0.08998 -0.07104 0.00000
16 11 -169.83564482 405.59960229 0.00000000 -0.00000 -0.00000 0.00000
17 12 -169.82950253 405.76673395 0.00925187 -0.00000 0.00000 0.04321
18 13 -169.81735744 406.09720202 0.00000000 0.00000 0.00000 0.00000
19 14 -169.81567589 406.14295698 0.00498163 -0.02593 -0.01821 0.00000
20 15 -169.81376836 406.19486083 0.00000000 -0.00000 0.00000 -0.00000
21 16 -169.81204070 406.24187047 0.00494890 0.01812 -0.02586 0.00000
22 17 -169.80681991 406.38392818 0.00000000 -0.00000 -0.00000 0.00000
23 18 -169.79772608 406.63137137 0.01209756 0.00000 -0.00000 -0.04935
24 19 -169.74853637 407.96982327 0.00000000 -0.00000 0.00000 -0.00000
25 20 -169.74401565 408.09283219 0.00113590 0.00000 0.00000 0.01510
26 21 -169.67330415 410.01689210 0.00000000 0.00000 -0.00000 0.00000
27 22 -169.67060344 410.09037844 0.00107912 0.00000 -0.00000 -0.01468
28 23 -169.65887737 410.40944479 0.00000000 0.00000 -0.00000 0.00000
29 24 -169.63235011 411.13125137 0.00601950 0.00000 0.00000 -0.03462
30 25 -169.07874371 426.19488170 0.00004203 0.00000 -0.00000 -0.00284
31 26 -169.07628789 426.26170433 0.00000000 0.00000 0.00000 -0.00000
32 27 -166.93991246 484.39247991 0.00003223 -0.00000 -0.00000 0.00233
33 28 -166.93767426 484.45338124 0.00000000 0.00000 -0.00000 -0.00000
You can identify the states from output files. For example, the coefficients of state 4 are:
1---- NOSI Coefficients Matrix (column vectors are eigenvectors) ----
2====================================================================
3 0 1 2 3 4
4 0 0.99999900 0.00000000 -0.00000000 0.00000000 -0.00000000
5 1 -0.00000000 -0.00573951 -0.00000102 0.00074472 -0.00000001
6 2 -0.00000000 0.00573951 0.00000102 0.00074472 -0.00000001
7 3 -0.00000000 0.00000132 0.00527620 -0.00000167 -0.00020742
8 4 -0.00000000 -0.00000132 -0.00527620 -0.00000167 -0.00020742
9 5 -0.00009224 -0.00000000 0.00000000 0.00000000 -0.00000000
10 6 -0.00009224 0.00000000 -0.00000000 0.00000000 -0.00000000
11 7 -0.00005050 0.00000004 -0.00000004 -0.00000003 0.00000003
12 8 -0.00005050 -0.00000004 0.00000004 -0.00000003 0.00000003
13 9 -0.01938433 0.00000002 0.00000006 0.00000027 0.00000011
14 10 -0.01938443 -0.00000002 -0.00000006 0.00000027 0.00000011
15 11 -0.01615554 -0.00000011 0.00000024 -0.00000053 0.00000224
16 12 -0.01615584 0.00000011 -0.00000024 -0.00000053 0.00000224
17 13 -0.00408296 0.00000017 -0.00000022 0.00000078 -0.00000210
18 14 -0.00408276 -0.00000017 0.00000022 0.00000078 -0.00000210
19 15 0.00000000 0.70440082 0.00016811 -0.70886826 0.00029439
20 16 0.00000000 -0.70440082 -0.00016811 -0.70886826 0.00029439
21 17 0.00000000 0.00007913 -0.70442320 0.00045204 0.70883620
22 18 0.00000000 -0.00007913 0.70442320 0.00045204 0.70883620
23 19 -0.00027387 0.00000004 -0.00000009 -0.00000007 0.00000003
24 20 -0.00027386 -0.00000004 0.00000009 -0.00000007 0.00000003
25 21 -0.00036762 0.00000357 -0.00000375 -0.00000369 0.00000380
26 22 -0.00036762 -0.00000357 0.00000376 -0.00000369 0.00000380
27 23 -0.00000001 -0.01231909 -0.00528893 -0.00894872 -0.00371633
28 24 -0.00000001 0.01231909 0.00528893 -0.00894872 -0.00371633
29 25 0.00000002 0.00424293 -0.01251586 0.00260869 -0.00878159
30 26 0.00000002 -0.00424293 0.01251586 0.00260869 -0.00878159
31 27 0.00040798 -0.00000375 0.00000392 0.00000362 -0.00000376
32 28 0.00040798 0.00000376 -0.00000392 0.00000362 -0.00000376
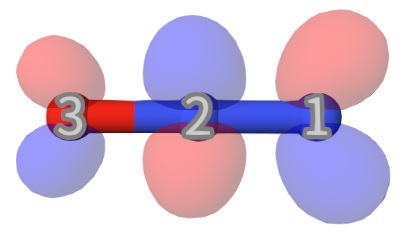
The largest coefficients for state 4 is \(0.70883620\phi_{17}+0.70883620\phi_{18}\), which is the combination of msdft-2-N-3-to-13-se.mwfn and its spin flipped one. So, this state is mainly the 3→13 single excitation, i.e. terminal-nitrogen \(1s\rightarrow\pi^*\) excitation (see below for MO 13, which is a \(\pi^*\) MO)
To plot the spectrum, you can use the script tools/plotspec.py provided by Qbics (or any tools you like). Assume you want to plot ```` First, copy this file to the same directory as the input file, and modify the following parameters:
1if __name__ == "__main__":
2 fn = "msdft-2-N-spectrum.txt" # Spectrum file name.
3 eL_eV = 400 # Lower energy limit.
4 eH_eV = 410 # Higher energy limit.
5 sigma_eV = 0.2 # Sigma value.
6 num_ps = 500 # Number of points.
7 use_angle = False # Whether to use angle dependence.
Here, we want to plot the spectrum from 400 (eL_eV) to 410 (eH_eV) eV, with a sigma value of 0.2 (sigma_eV) and 500 (num_ps) points. You can change these parameters to get the desired spectrum.
Tip
Please cite this paper, if you use this script and formular in it:
The N and O K-edge XAS spectra as well as experimental data are shown below:
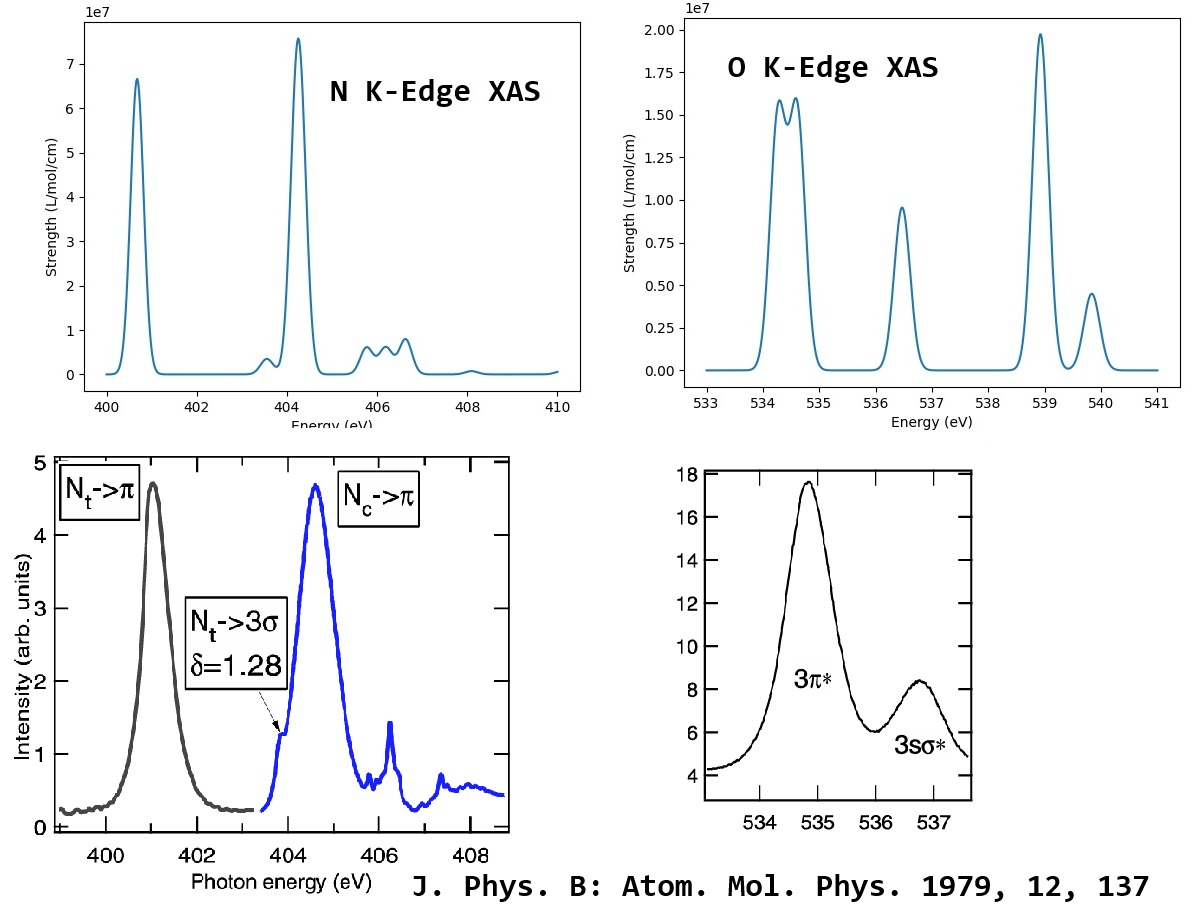
We can see that, MSDFT can give quite good results for N and O K-edge XAS!