Tip

All input files can be downloaded: Files.

tddft

This keyword defines how to perform time-dependent DFT (TDDFT) calculation.

Options

type

Value	TDDFT Standard TDDFT.
	TDA TDDFT with Tamm-Dancoff approximation (TDA).
	RTDDFT Restricted TDDFT.
	UTDDFT Unrestricted TDDFT.
	XTDDFT Spin-adaptive TDDFT.
	RTDA Restricted TDA.
	UTDA Unrestricted TDA.
	XTDA Spin-adaptive TDA.
Default	TDDFT

The type of TDDFT calculations. TDA is an approximate case of TDDFT. For closed-shell systems, RTDDFT and RTDA are the best choices. For closed- and open-shell systems, UTDDFT and UTDA are available. For open-shell systems, XTDDFT and XTDA are also available. If TDDFT or TDA is used, a suitable method will be automatically selected.

spin_flip

Value	None No spin flipping is performed.
	Up Flip beta electrons to alpha ones.
	Down Flip alpha electrons to beta ones.
Default	None

Spin flipping way for the excited states.

num_states

Value	An integer.
Default	5

The number of excited states to be calculated.

max_it

Value	An integer.
Default	100

The maximum number of Davidson iterations for the TDDFT calculation. If TDDFT fails to converge, you can try to increase this number.

dim_trials

Value	An integer.
Default	50

The maximum dimension of trial vectors. If TDDFT fails to converge, you can try to increase this number.

energy_cov

Value	A real number.
Default	1.E-7

The energy convergence threshold for the TDDFT calculation.

vec_cov

Value	A real number.
Default	1.E-5

The excited state vector convergence threshold for the TDDFT calculation.

precondition_threshold

Value	A real number.
Default	1.E-8

The precondition convergence threshold for the TDDFT calculation.

print_coeff_threshold

Value	A real number.
Default	0.01

Print the excited state coefficients when the absolute value is larger than this threshold.

transxtdvec

Transform the excited state vectors from alpha/beta to spin-adapted ones.

Theoretical Background

Time-dependent DFT (TDDFT) is a powerful tool for studying the electronic structure of molecules and materials. It is a time-dependent extension of density functional theory (DFT), which allows for the calculation of excited states and transition properties.

Input Examples

Example: TDDFT Calculation of HCHO

In this example, we will perform a TDDFT calculation of HCHO at TD-B3LYP/cc-pVTZ level of theory. The input file is as follows:

tddft-1.inp

basis
    cc-pvtz
end

scf
    charge      0
    spin2p1     1
    type        R
end

mol
    C -0.000756 -0.520733 0.
    H  0.935697 -1.111766 0.
    H -0.939631 -1.107897 0.
    O  0.001792  0.678123 0
end

tddft
    type                   tddft
    num_states             10
    max_it                 100
    dim_trials             50
    print_coeff_threshold  0.01
end

task
    tddft b3lyp
end

After running the calculation, you will find the following lines:

tddft-1.out

#1: Absolute energy = -114.39668857 Hartree
   Excited energy = 4.1600 eV; wavelength = 298.04 nm, oscillator strength = 0.0000
   Transition dipole moment (a.u.):  -0.00000  -0.00000  -0.00000
   CV(0)    8 -->    9: Coefficient =   -0.9512, Percentage =   99.7 %, IPA =     6.0538 eV
#2: Absolute energy = -114.26455102 Hartree
   Excited energy = 7.7556 eV; wavelength = 159.86 nm, oscillator strength = 0.0917
   Transition dipole moment (a.u.):   0.69575  -0.00144  -0.00000
   CV(0)    8 -->   10: Coefficient =    0.9803, Percentage =   99.1 %, IPA =     8.7346 eV
#3: Absolute energy = -114.20726662 Hartree
   Excited energy = 9.3144 eV; wavelength = 133.11 nm, oscillator strength = 0.0004
   Transition dipole moment (a.u.):   0.00000  -0.00000   0.03936
   CV(0)    6 -->    9: Coefficient =    0.9615, Percentage =   99.0 %, IPA =    11.0312 eV

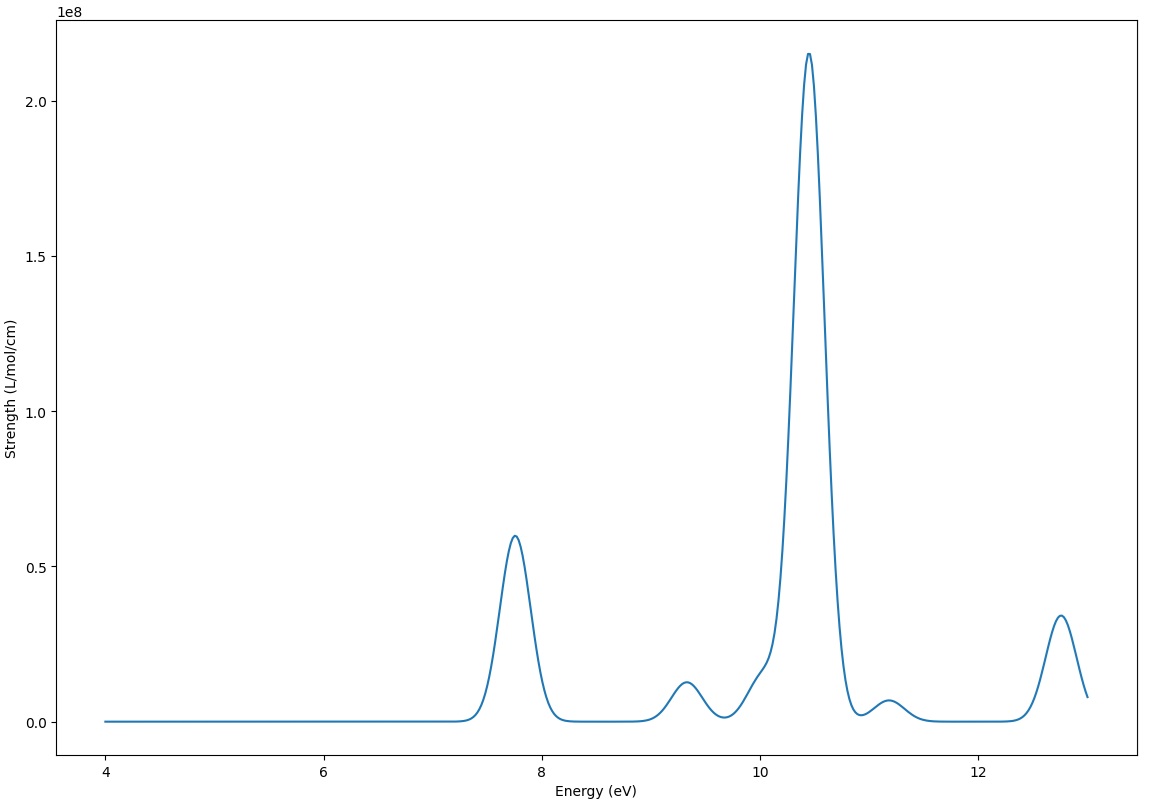
You can find excited state energies, oscillator strengths, transition dipole moments, and orbital transition coefficients.

You can also find the spectrum file tddft-1-spectrum.txt.

You can plot the spectrum using a script provided by Qbics, i.e., tools/plotspec.py. Copy this file to the same directory as the input file, and modify the following parameters:

plotspec.py

if __name__ == "__main__":
    fn = "tddft-1-spectrum.txt"       # Spectrum file name.
    eL_eV = 4                   # Lower energy limit.
    eH_eV = 13                  # Higher energy limit.
    sigma_eV = 0.2              # Sigma value.
    num_ps = 500                # Number of points.
    use_angle = False           # Whether to use angle dependence.
    incident_angles = [i*30 for i in range(4)] # Incident angles.

• Line 2: Change the spectrum file name.

• Line 3,4: Change the lower and upper energy limit.

• Line 5: Change the sigma value.

• Line 6: Change the number of points. The larger the number, the smoother the spectrum.

• Line 7: Whether to use angle dependence.

• Line 8: Incident angles.

Then, you can run the script using the following command:

plotspec.py

$ python plotspec.py

You will find following spectrum plot: