All input and output files can be downloaded here.
TSO-DFT for Excited State Energies
TSO-DFT (TSO = target state optimization) is an originally developed powerful method for calculating electronic excited and diabatic states. It is a single-determinant method so you can study an excited or diabatic state very efficiently. For charge transfer, core, and doubly excitations, TSO-DFT outperforms TDDFT significantly!
In this tutorial, we will describe how to compute electronic excited states for molecules.
For details and performance of TSO-DFT, please refer to the following paper. This should also be cited if you use TSO-DFT in your research work.
- Zhang, J.; Tang, Z.; Zhang, X.; Zhu, H.; Zhao, R.; Lu, Y.; Gao, J. Target State Optimized Density Functional Theory for Electronic Excited and Diabatic States. J. Chem. Theory Comput. 2023, 19, 1777-1789.
TSO-DFT is a highly flexible method for excitation and diabatization. You can realize any electronic state with orbital subspace partition.
Core Excitated State
We consider the core excitation of formaldehyde. We use this as the first example because it is simple for us to understand how TSO-DFT works but also an "excellent" example where TDDFT completely fails!
Ground State
First, a ground state calculation is carried out using the following input:
basis
element
H cc-pVTZ
C cc-pCVTZ
O cc-pCVTZ
end
scf
charge 0
spin2p1 1
end
mol
C -0.000756 -0.520733 0.
H 0.935697 -1.111766 0.
H -0.939631 -1.107897 0.
O 0.001792 0.678123 0
end
task
energy b3lyp
endAfter calculation by
$ qbics hcho-gs.inp -n 4 > hcho-gs.out we get a ground state wave function hcho-gs.mwfn. Let's visualize its orbitals with Multiwfn, we will find this:
| Index | Occupation | Property |
|---|---|---|
| 2 | doubly occupied | 1s core orbital of C1 |
| 7 | doubly occupied | π bonding orbital |
| 8 | doubly occupied | n nonbonding orbital |
| 9 | unoccupied | π* anti-bonding orbital |
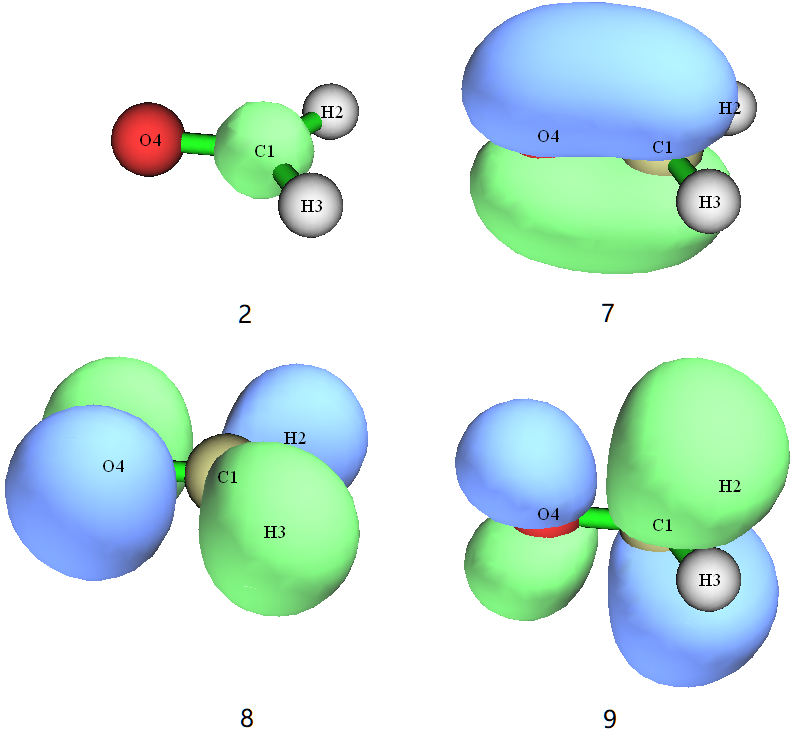
We can also know from output file hcho-gs.out that there are totally 16 electrons and 114 basis functions, and the ground state energy is -114.55175795 Hartree.
C 1s → π* Excited State
Now we want to study the state when one 1s electron of carbon is excited to a π* orbital, which is MO 2 and 9, respectively. In this case, the powerful TSO-DFT should be used, with the following input:
basis
element
H cc-pVTZ
C cc-pCVTZ
O cc-pCVTZ
end
scf
charge 0
spin2p1 1
type U # For TSO-DFT, unrestricted SCF is preferred.
do_tso
end
scfguess
type mwfn
file hcho-gs.mwfn
orb 16 1 1-113 : 1 3-114
orb 0 1 114 : 2
end
mol
C -0.000756 -0.520733 0.
H 0.935697 -1.111766 0.
H -0.939631 -1.107897 0.
O 0.001792 0.678123 0
end
task
energy b3lyp
endNow we will explain the key points in hcho-c1se.inp:
do_tsoThis option inscf ... endblock will turn on TSO calculations.type UFor TSO-DFT, it is preferred to using unrestricted SCF.- A reference state is needed. In this case, the ground state of formaldehyde, so the initial guess in
scfguess ... endblock should betype mwfnandfile hcho-gs.mwfn.
TSO-DFT can only use 2 kind of initial guess: type mwfn and type fragden. The latter will be useful in diabatic state studies.
orb is the most important keyword in TSO calculations. There can be arbitrary number of orb, meaning that orbitals are partitioned into several subspaces. Orbitals from different subspaces will not mix. The format of orb is
orb num_electrons spin_multiplicity alpha_MO_indices : beta_MO_indices
For example, orb 16 1 1-113 : 1 3-114 means that in this subspace, there are 16 electrons, the spin multiplicity is 1. The alpha orbitals are 1,2,3,...,113, and the beta orbital are 1,3,...,114. So, orb 0 1 114 : 2 defines another subspace, which has 0 electrons, the alpha orbitals is 114, and the beta orbitals is only 2.
Why do we partition the orbitals into 2 subspaces like this? Let's see the figure below.
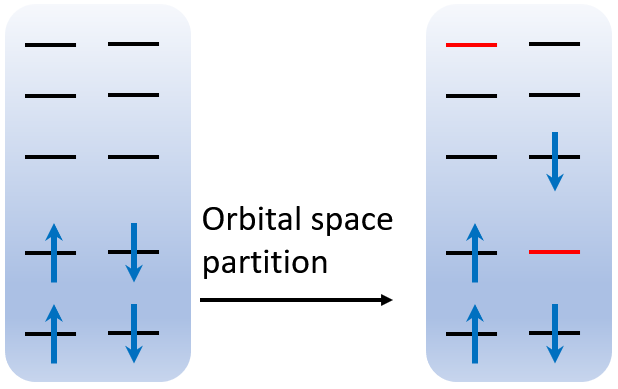
The first and second subspace are rendered by black and red color, respectively. Since beta orbital 2 is removed, the aufbau occupation of 15 electrons will automatically skip the C 1s orbital, so the π* orbital, i.e. MO 9, is also occupied automatically. However, the number of alpha and beta orbitals must be identical, so one can remove the highest alpha orbital, which is 114. These remaining orbitals will be collected to form another subspace, none of which is occupied. In this case, a C 1s → π* excited state is successfully constructed.
Let's run this calculation:
$ qbics hcho-c1sex.inp -n 4 > hcho-c1sex.out We can get the C 1s ionized state wave function hcho-c1sex.mwfn and output file hcho-c1sex.out. We can find that
Molecular Orbitals
==================
k = Gamma
Alpha HOMO-LUMO (8-9) gap: 5.827 eV
Beta HOMO-LUMO (8-9) gap: 6.141 eV
Alpha Alpha Beta Beta
# Occupancies Energies/Hartree Occupancies Energies/Hartree
1 1.000 -19.13049258 1.000 -19.14916538
2 1.000 -12.32577074 1.000 -1.11992044
3 1.000 -1.10653786 1.000 -0.70203028
4 1.000 -0.70362987 1.000 -0.55634086
5 1.000 -0.56613413 1.000 -0.49715471
6 1.000 -0.48311622 1.000 -0.48046027
7 1.000 -0.41628076 1.000 -0.28713576
8 1.000 -0.27184459 1.000 -0.20773869
9 0.000 -0.05770604 0.000 0.01794976
10 0.000 0.01275050 0.000 0.07049694
Final total energy: -104.06138400 HartreeFrom molecular orbitals, we can find that one C 1s orbital is indeed excited, and the energy is -104.06138400 Hartree.
Now the C state energy of formaldehyde is: − 104.06138400 − ( − 114.55175795) = 10.490374 Hartree, i.e., 285.45 eV. For comparison:
| Method | C 1s → π* Excitation Energy |
|---|---|
| TSO-B3LYP | 285.5 eV |
| TD-B3LYP | 275.2 eV |
| Experiment | 286.0 eV |
Obviously, TSO give excellent results!
Doubly Excited States
Doubly excited state means that two electrons are excited simultaneously from the ground state. Popular TDDFT implemented with adiabatic approximation cannot be used to study double excited states. However, this can be easily done with TSO.
For formaldehyde, we consider the doubly excited state n2 → (π*)2, i.e. 2 electrons from MO 8 are excited to MO 9. The input file is:
basis
element
H cc-pVTZ
C cc-pCVTZ
O cc-pCVTZ
end
scf
charge 0
spin2p1 1
type U # For TSO-DFT, unrestricted SCF is preferred.
do_tso
end
scfguess
type mwfn
file hcho-gs.mwfn
orb 16 1 1-7 9-114 : 1-7 9-114
orb 0 1 8 : 8
end
mol
C -0.000756 -0.520733 0.
H 0.935697 -1.111766 0.
H -0.939631 -1.107897 0.
O 0.001792 0.678123 0
end
task
energy b3lyp
endWe can see that, orb 16 1 1-7 9-114 : 1-7 9-114 defines a subspace that both alpha and beta MO 8 are removed, so the last alpha and beta electrons will automatically occupy MO 9. The double excitation is achieved. Run the calculation:
$ qbics hcho-de.inp -n 4 > hcho-de.out The energy is -114.15907187 Hartree, so the double excitation energy is: − 114.15907187 − ( − 114.55175795) = 0.39268 Hartree, i.e., 10.68 eV. For comparison:
| Method | n2 → (π*)2 Excitation Energy |
|---|---|
| TSO-B3LYP | 10.68 eV |
| EOM-CC | 10.34 eV |
Obviously, our TSO-DFT is highly accurate!
For a theoretical explaination of the excellent performance of TSO-DFT, please refer to the TSO paper:
- Zhang, J.; Tang, Z.; Zhang, X.; Zhu, H.; Zhao, R.; Lu, Y.; Gao, J. Target State Optimized Density Functional Theory for Electronic Excited and Diabatic States. J. Chem. Theory Comput. 2023, 19, 1777-1789.