Tip

All input and output files can be downloaded here.

TSO-DFT for Excited State Energies

TSO-DFT (TSO = target state optimization) is an originally developed powerful method for calculating electronic excited and diabatic states. It is a single-determinant method so you can study an excited or diabatic state very efficiently. For charge transfer, core, and doubly excitations, TSO-DFT outperforms TDDFT significantly!

In this tutorial, we will describe how to compute electronic excited states for molecules.

Tip

For details and performance of TSO-DFT, please refer to the following paper. This should also be cited if you use TSO-DFT in your research work.

Zhang, J.; Tang, Z.; Zhang, X.; Zhu, H.; Zhao, R.; Lu, Y.; Gao, J. Target State Optimized Density Functional Theory for Electronic Excited and Diabatic States. J. Chem. Theory Comput. 2023, 19, 1777-1789.

TSO-DFT is a highly flexible method for excitation and diabatization. You can realize any electronic state with orbital subspace partition.

Core Excitated State

We consider the core excitation of formaldehyde. We use this as the first example because it is simple for us to understand how TSO-DFT works but also an “excellent” example where TDDFT completely fails!

Ground State

First, a ground state calculation is carried out using the following input:

hcho-gs.inp

basis
    element
    H cc-pVTZ
    C cc-pCVTZ
    O cc-pCVTZ
end

scf
    charge      0
    spin2p1     1
end

mol
    C -0.000756 -0.520733 0.
    H  0.935697 -1.111766 0.
    H -0.939631 -1.107897 0.
    O  0.001792  0.678123 0
end

task
    energy b3lyp
end

After calculation by

$ qbics hcho-gs.inp -n 4 > hcho-gs.out

we get a ground state wave function hcho-gs.mwfn. Let’s visualize its orbitals with Multiwfn, we will find this:

Index	Occupation	Property
2	doubly occupied	1s core orbital of C1
7	doubly occupied	π bonding orbital
8	doubly occupied	n nonbonding orbital
9	unoccupied	π* anti-bonding orbital

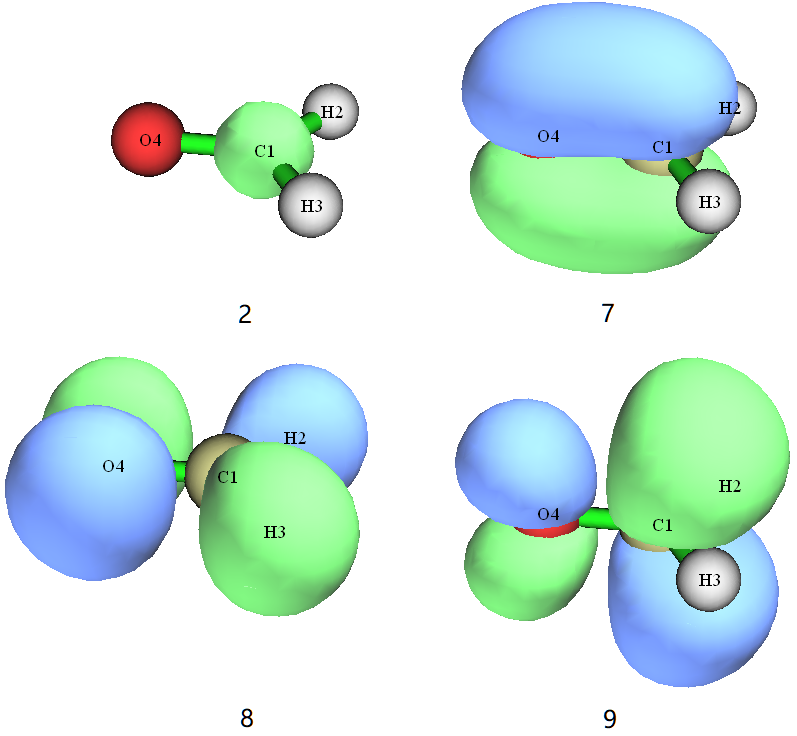
We can also know from output file hcho-gs.out that there are totally 16 electrons and 114 basis functions, and the ground state energy is -114.55175795 Hartree.

C 1s→π* Excited State

Now we want to study the state when one 1s electron of carbon is excited to a π* orbital, which is MO 2 and 9, respectively. In this case, the powerful TSO-DFT should be used, with the following input:

hcho-c1se.inp

basis
    element
    H cc-pVTZ
    C cc-pCVTZ
    O cc-pCVTZ
end

scf
    charge      0
    spin2p1     1
    type        U # For TSO-DFT, unrestricted SCF is preferred.
    do_tso
end

scfguess
    type mwfn
    file hcho-gs.mwfn
    orb 16 1 1-113 : 1 3-114
    orb  0 1 114 : 2
end

mol
    C -0.000756 -0.520733 0.
    H  0.935697 -1.111766 0.
    H -0.939631 -1.107897 0.
    O  0.001792  0.678123 0
end

task
    energy b3lyp
end

Now we will explain the key points in hcho-c1se.inp:

do_tso This option in scf ... end block will turn on TSO calculations.
type U For TSO-DFT, it is preferred to using unrestricted SCF.
A reference state is needed. In this case, the ground state of formaldehyde, so the initial guess in scfguess ... end block should be type mwfn and file hcho-gs.mwfn.

Attention

TSO-DFT can only use 2 kind of initial guess: type mwfn and type fragden. The latter will be useful in diabatic state studies.

orb is the most important keyword in TSO calculations. There can be arbitrary number of orb, meaning that orbitals are partitioned into several subspaces. Orbitals from different subspaces will not mix. The format of orb is

orb num_electrons spin_multiplicity alpha_MO_indices : beta_MO_indices

For example, orb 16 1 1-113 : 1 3-114 means that in this subspace, there are 16 electrons, the spin multiplicity is 1. The alpha orbitals are 1,2,3,…,113, and the beta orbital are 1,3,…,114. So, orb 0 1 114 : 2 defines another subspace, which has 0 electrons, the alpha orbitals is 114, and the beta orbitals is only 2.

Why do we partition the orbitals into 2 subspaces like this? Let’s see the figure below.

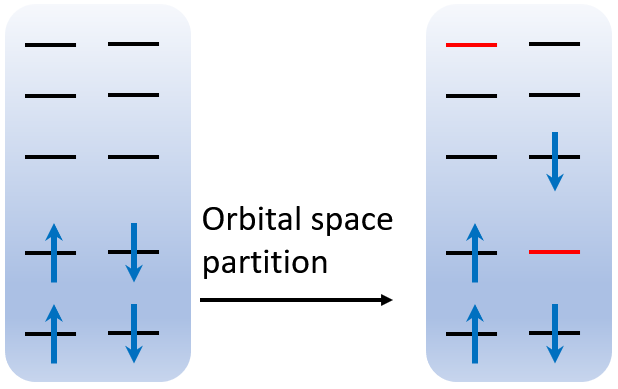
The first and second subspace are rendered by black and red color, respectively. Since beta orbital 2 is removed, the aufbau occupation of 15 electrons will automatically skip the C 1s orbital, so the π* orbital, i.e. MO 9, is also occupied automatically. However, the number of alpha and beta orbitals must be identical, so one can remove the highest alpha orbital, which is 114. These remaining orbitals will be collected to form another subspace, none of which is occupied. In this case, a C 1s→π* excited state is successfully constructed.

Let’s run this calculation:

$ qbics hcho-c1sex.inp -n 4 > hcho-c1sex.out

We can get the C 1s ionized state wave function hcho-c1sex.mwfn and output file hcho-c1sex.out. We can find that

hcho-c1sex.out

Molecular Orbitals
==================
k = Gamma
Alpha HOMO-LUMO (8-9) gap: 5.827 eV
Beta HOMO-LUMO (8-9) gap:  6.141 eV
              Alpha                Alpha          Beta                 Beta
    #   Occupancies     Energies/Hartree   Occupancies     Energies/Hartree
    1         1.000         -19.13049258         1.000         -19.14916538
    2         1.000         -12.32577074         1.000          -1.11992044
    3         1.000          -1.10653786         1.000          -0.70203028
    4         1.000          -0.70362987         1.000          -0.55634086
    5         1.000          -0.56613413         1.000          -0.49715471
    6         1.000          -0.48311622         1.000          -0.48046027
    7         1.000          -0.41628076         1.000          -0.28713576
    8         1.000          -0.27184459         1.000          -0.20773869
    9         0.000          -0.05770604         0.000           0.01794976
   10         0.000           0.01275050         0.000           0.07049694
Final total energy:        -104.06138400 Hartree

From molecular orbitals, we can find that one C 1s orbital is indeed excited, and the energy is -104.06138400 Hartree.

Now the C state energy of formaldehyde is: \(-104.06138400-(-114.55175795) = 10.490374\) Hartree, i.e., 285.45 eV. For comparison:

Method	C 1s→π* Excitation Energy
TSO-B3LYP	285.5 eV
TD-B3LYP	275.2 eV
Experiment	286.0 eV

Obviously, TSO give excellent results!

Doubly Excited States

Doubly excited state means that two electrons are excited simultaneously from the ground state. Popular TDDFT implemented with adiabatic approximation cannot be used to study double excited states. However, this can be easily done with TSO.

For formaldehyde, we consider the doubly excited state \(n^2\rightarrow (\pi^*)^2\), i.e. 2 electrons from MO 8 are excited to MO 9. The input file is:

hcho-de.inp

basis
    element
    H cc-pVTZ
    C cc-pCVTZ
    O cc-pCVTZ
end

scf
    charge      0
    spin2p1     1
    type        U # For TSO-DFT, unrestricted SCF is preferred.
    do_tso
end

scfguess
    type mwfn
    file hcho-gs.mwfn
    orb 16 1 1-7 9-114 : 1-7 9-114
    orb  0 1 8 : 8
end

mol
    C -0.000756 -0.520733 0.
    H  0.935697 -1.111766 0.
    H -0.939631 -1.107897 0.
    O  0.001792  0.678123 0
end

task
    energy b3lyp
end

We can see that, orb 16 1 1-7 9-114 : 1-7 9-114 defines a subspace that both alpha and beta MO 8 are removed, so the last alpha and beta electrons will automatically occupy MO 9. The double excitation is achieved. Run the calculation:

$ qbics hcho-de.inp -n 4 > hcho-de.out

The energy is -114.15907187 Hartree, so the double excitation energy is: \(-114.15907187-(-114.55175795) = 0.39268\) Hartree, i.e., 10.68 eV. For comparison:

Method	\(n^2\rightarrow (\pi^*)^2\) Excitation Energy
TSO-B3LYP	10.68 eV
EOM-CC	10.34 eV

Obviously, our TSO-DFT is highly accurate!

Tip

For a theoretical explaination of the excellent performance of TSO-DFT, please refer to the TSO paper:

Zhang, J.; Tang, Z.; Zhang, X.; Zhu, H.; Zhao, R.; Lu, Y.; Gao, J. Target State Optimized Density Functional Theory for Electronic Excited and Diabatic States. J. Chem. Theory Comput. 2023, 19, 1777-1789.