Paper for target state optimization (TSO) DFT is published on JCTC!
目标态优化(TSO)方法
TSO方法简单介绍:
TSO(Target State Optimization)是一种用于探索电子激发构型和局部从属态(diabatic states)的灵活自洽场方法。 其关键的实现思路在于,将分子轨道根据目标态的激发或局域化模式划分为不同的子空间。这样的处理方式不会将不同子空间的轨道相互混合,可以确保激发态或从属态配置的行列式波函数可以像基态程序一样进行变分优化。
TSO方法的优势:
- 避免了传统的ΔSCF方法中回到基态或其他低能态的可能性。
- TSO方法可以应用于Hartree-Fock理论和Kohn-Sham密度泛函理论(DFT)。
TSO方法的部分示例(自论文原文中提取)
1、价激发态
由于传统的时变密度泛函理论(TD-DFT)在处理价激发态方面相当可靠,因此,将TSO方法的计算结果与TD-DFT进行比较具有重要的研究意义。 在本文中,我们通过TSO方法对中等大小有机分子的激发态能量进行了计算,并与最近的一项基准研究结果进行了比较。在下表中,我们展示了部分数据,体现了TSO方法与TD-DFT方法在激发态能量计算中的表现差异:
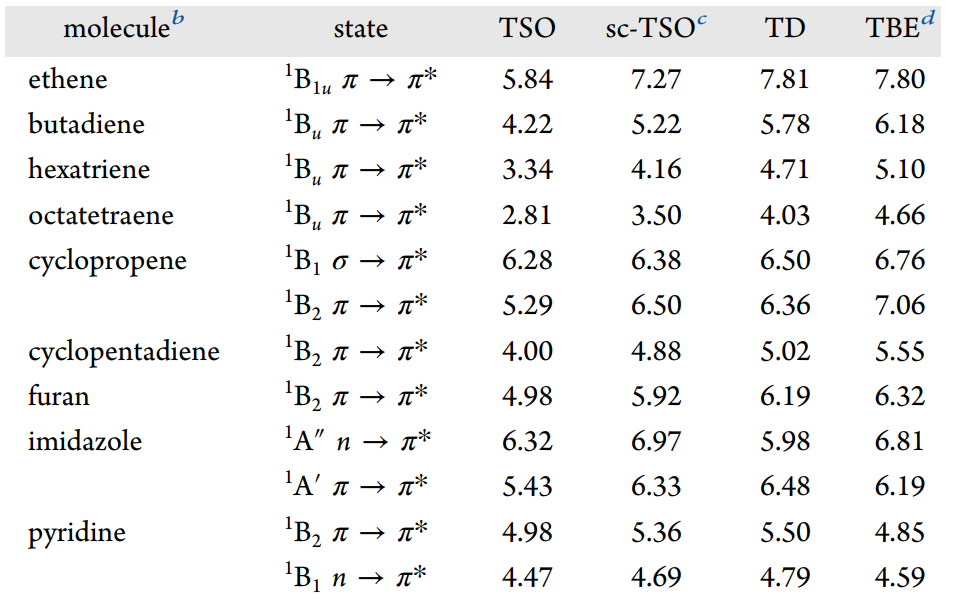
其中,sc-TSOc 表示通过正文公式 (24) 对 TSO-DFT 方法计算出的能量进行了校正。TBEd 则表示从正文引用的参考文献 110 中获得的理论最佳估计数据,用于作为比较基准。
通过本文的研究,我们发现TSO方法与TD-DFT在激发能量计算中的精度相当,均方根误差(RMSE)分别为0.50 eV和0.40 eV,最大误差主要出现在烯烃中。然而,由于自旋污染,自旋混合的TSO-DFT结果误差较大。
2、核心激发态
核心激发态(即核心电子的激发)对理解局部环境中的化学相互作用至关重要。 本文中,我们采用TSO-B3LYP/cc-pCVTZ方法对小型有机化合物的1s核心轨道电子的电离能和激发能进行了计算,并与传统的时间依赖密度泛函理论(TD-DFT)计算结果进行了比较。下图展示了部分理论计算结果对比数据。
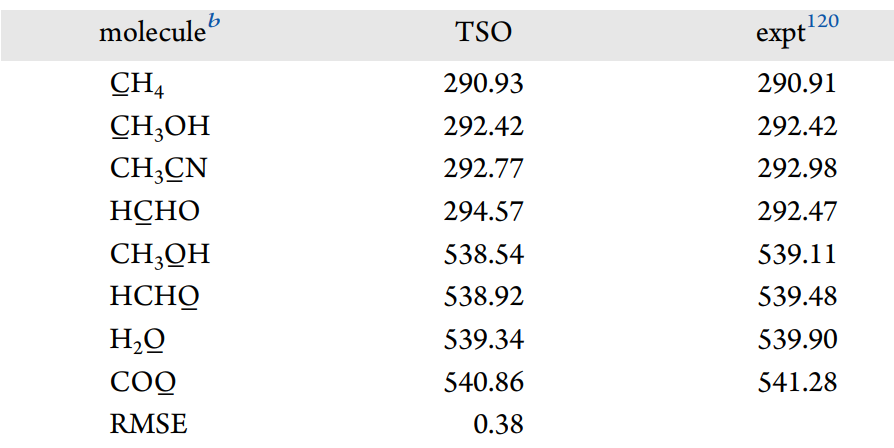
其中,将从正文引用的 参考文献 120 数据作为比较基准。
结果表明,TSO方法对核心激发能的计算结果与实验数据非常接近,均方根误差(RMSE)为0.38 eV(电离能)和0.56 eV(激发能)。相比之下,TD-DFT方法在核心激发能方面存在显著的系统性误差,平均过高12.49 eV。因此,TSO方法在核心激发能的计算上优于TD-DFT。